Fast and Robust: Task Sampling with Posterior and Diversity Synergies for Adaptive Decision-Makers in Randomized Environments

Authors: Yun Qu, Qi (Cheems) Wang, Yixiu Mao, Yiqin Lv, Xiangyang Ji
Affiliation: Tsinghua University
Link: https://github.com/thu-rllab/PDTS/*

🚀 Introduction: Toward Fast and Robust Adaptation

Modern adaptive decision-makers like reinforcement learning agents or foundation models often operate in highly dynamic environments. A long-standing goal is to ensure these agents can robustly adapt to unseen or out-of-distribution (OOD) scenarios. However, methods like Conditional Value-at-Risk (CVaR), though robust, suffer from intensive computational cost due to exhaustive task evaluation.

To address this challenge, the authors introduce Posterior and Diversity Task Sampling (PDTS), a new method for robust active task sampling that achieves stronger adaptation robustness with minimal overhead. The key idea is to treat task selection as a secret MDP and leverage posterior sampling and diversity regularization to efficiently select challenging tasks.

🧠 Motivation: What Makes Adaptation Difficult?

In meta-reinforcement learning (Meta-RL) and domain randomization (DR), agents must generalize to new MDPs sampled from a task distribution. Real-world deployments (e.g., autonomous driving or robotics) demand robustness to rare but high-risk events. However, sampling tasks uniformly from a task distribution misses these critical edge cases.

To bridge this gap, PDTS prioritizes task selection based on: - Predicted adaptation risk (from a learned risk predictive model), - Task diversity (to avoid overfitting narrow regions), - Posterior sampling (to simplify and optimize task sampling).

This framework is analyzed in a theoretical task-selection MDP abstraction and empirically improves robustness across multiple benchmarks.

(a) General RATS in risk-averse decision-making. The pipeline involves amortized evaluation of task difficulties, robust subset selection, policy optimization in the MDP batch, and risk predictive models' update. [fire: updates; snow: evalluation]
(b) PDTS as a RATS method. PDTS treats task subsets as bandit arms, evaluates values through posterior sampling, and solves a regularized problem.

⚙️ Methodology: From Theory to Practical PDTS

🧩 Setting: Meta-RL and Domain Randomization

Each task is modeled as an MDP $\tau \in \mathbb{R}^d$ with support data $\mathcal{D}_\tau^S$ and query data $\mathcal{D}_\tau^Q$. The adaptation risk is measured by $\ell(\mathcal{D}_\tau^Q, \mathcal{D}_\tau^S; \theta)$, and the goal is to optimize for worst-case performance under a task distribution $p(\tau)$.

📈 Step 1: Risk Prediction via Variational Generative Model

A VAE-style generative model predicts adaptation risk: $\mathbb{E}_{q_\phi(z_t|H_t)}[p_\psi(\ell|\tau, z_t)]$ where $H_t$ is the task history and $z_t$ summarizes adaptation dynamics. This amortizes costly environment interactions.

🎯 Step 2: Robust Subset Selection via i-MAB

The task space is viewed as an infinite-armed bandit (i-MAB): - State: model parameters $\theta$ - Action: select task batch $\mathcal{T}_{t+1}^\mathcal{B}$ - Reward: reduction in CVaR - Goal: maximize cumulative robustness gain

PDTS samples tasks based on: $ \mathcal{A}(\mathcal{T}^\mathcal{B}) + \gamma \cdot \text{Diversity}(\mathcal{T}^\mathcal{B}) $ with diversity measured via pairwise distance in $\tau$-space, which addresses the concentration issue in MPTS.

$MPTS's Performance Collapse with Greater $\hat{\mathcal{B}}$. We report the performance collapses of MPTS on Walker2dVel in the case $\hat{\mathcal{B}}=8\mathcal{B}$. The task sampling frequency reveals the presence of the concentration issue.$

🔄 Step 3: Posterior Sampling Instead of UCB

Unlike UCB-based MPTS, PDTS uses posterior sampling: $ z_t \sim q_\phi(z_t | H_t), \quad \ell_i \sim p_\psi(\ell | \tau_i, z_t) $ This avoids dedicated hyperparameter tradeoff and encourages stochastic optimism.

PDTS Algorithm

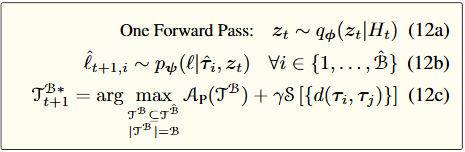
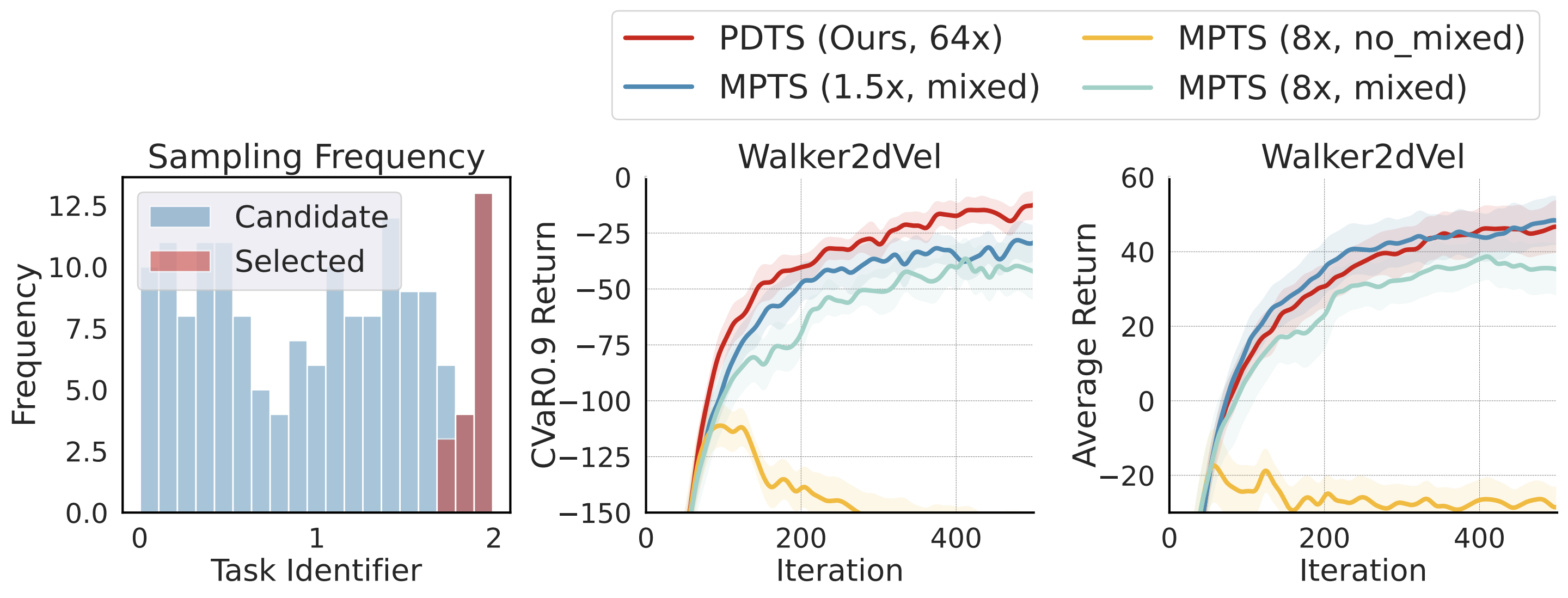
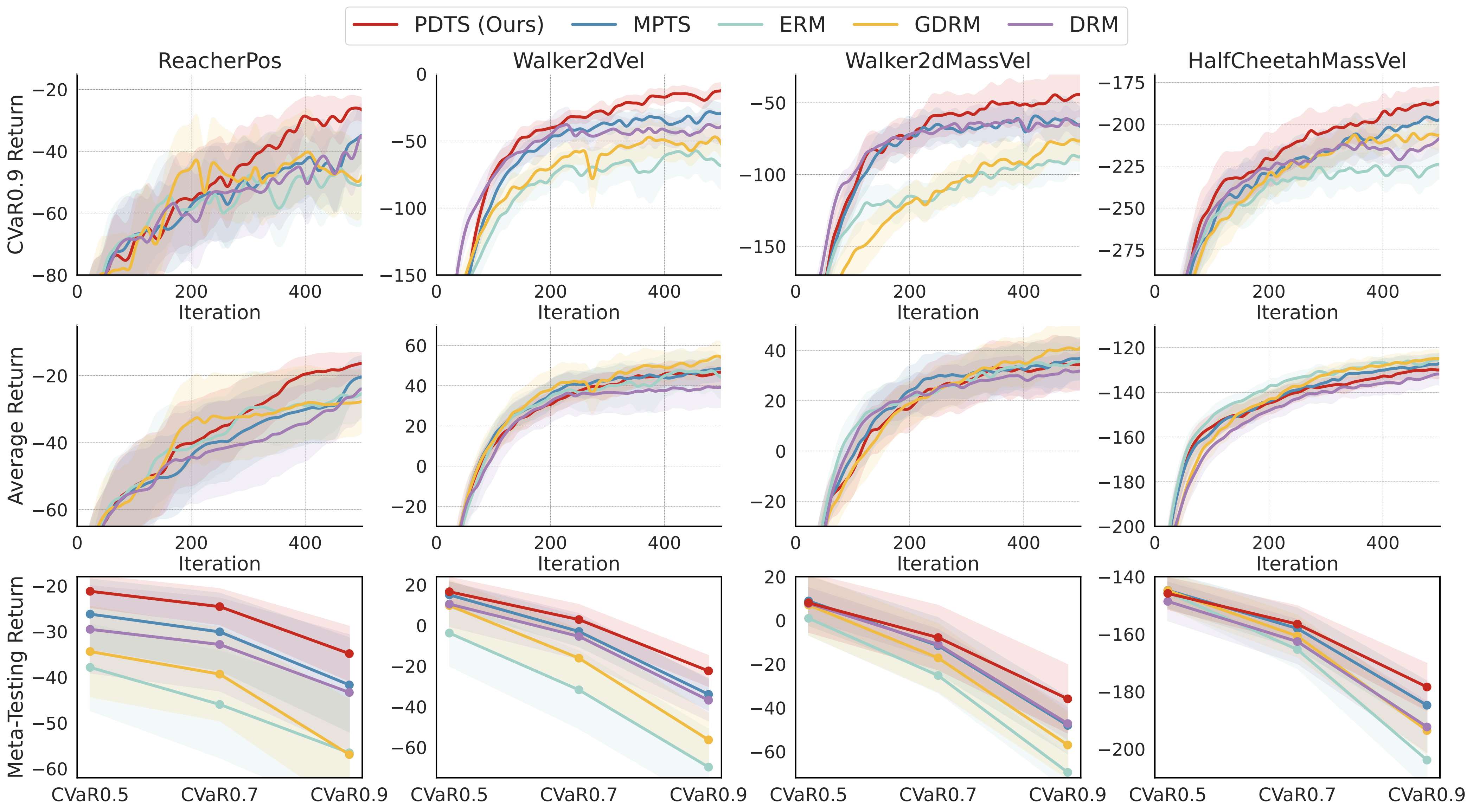
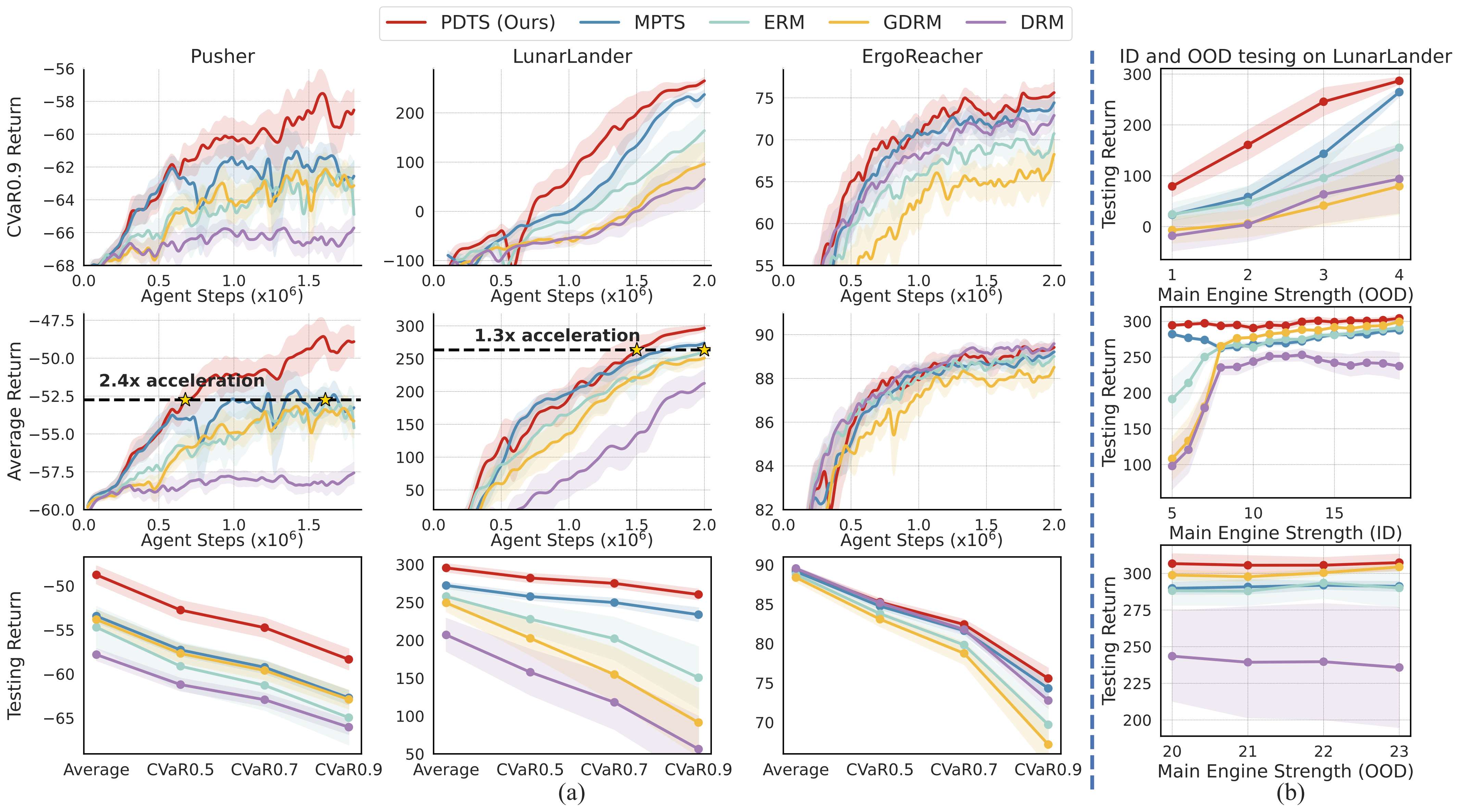
📊 Results: Faster and More Reliable Learning

PDTS is benchmarked across: - Meta-RL: MuJoCo tasks like Reacher, Walker2d, HalfCheetah. - Physical DR: Domain randomization with randomized physics properties, including tasks like Pusher, LunarLander, and ErgoReacher. - Visual DR: LiftPegUpright (light randomized), AnymalCReach (goal randomized).

$Meta-RL results. The top depicts the cumulative return curves for $\text{CVaR}_{0.9}$ validation MDPs during meta-training; the middle shows the average cumulative returns curves during meta-training; and the bottom presents the meta-testing results with various $\alpha$.$

$Physical Robotics DR results. (a) The top shows the cumulative return curves for $\text{CVaR}_{0.9}$ validation MDPs during training; the middle displays the average cumulative return curves across all validation MDPs during training; and the bottom presents the test results at various $\text{CVaR}_{\alpha}$. (b) We evaluate the trained policies in both in-distribution (ID) and out-of-distribution (OOD) domains on LunarLander, reporting the average returns for each sampled task.$

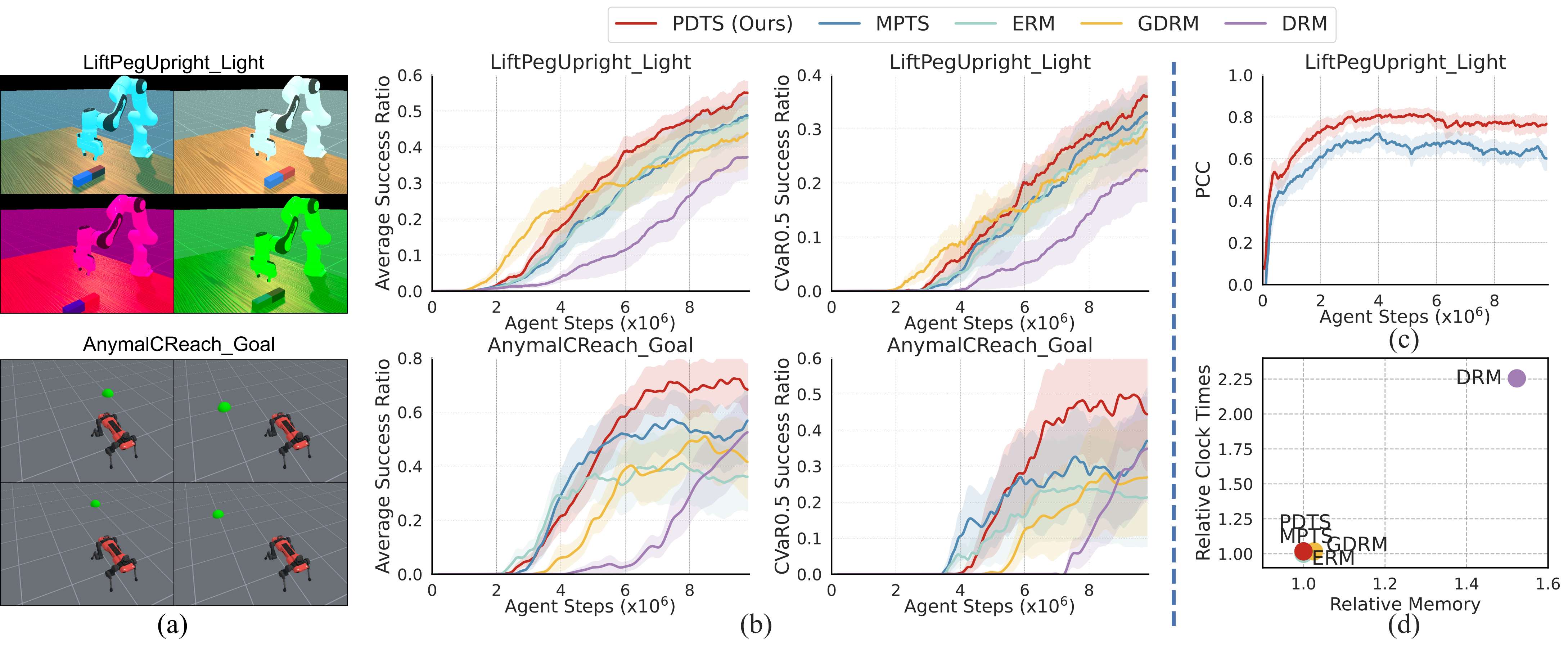
$Visual Robotics DR results. (a) Illustrations of two scenarios. (b) Curves of the average success ratio and the $\text{CVaR}_{0.5}$ success ratio on validation tasks during training. (c) Training curves of PCC values between predicted and true episode returns. (d) Memory cost and clock time relative to ERM during meta-training.$

✅ Highlights:

Best [email protected] performance in almost all tasks.
Outperforms DRM and MPTS without expensive task evaluation and hyperparameters tuning.
Superior exploration with larger candidate batches ($\hat{\mathcal{B}} = 64 \cdot \mathcal{B}$).
Accelerated learning (2.4× faster in Pusher, 1.3× in LunarLander).
OOD generalization improves dramatically (e.g., in LunarLander).
Minimal overhead: runtime increase is negligible compared to traditional risk-averse baselines DRM.

🧠 Insights and Future Work

PDTS provides a plug-and-play solution for robust adaptive learning in randomized environments. By integrating posterior inference and diversity-regularized selection, it achieves nearly worst-case optimization without sacrificing scalability.

Future directions: - Enhanced risk models with better uncertainty quantification, - Integration with multimodal agents or language models, - Real-world deployment in robotics and decision-critical AI.

📌 Conclusion

The PDTS framework redefines how adaptive agents should sample tasks for training. Instead of brute-force evaluation or handcrafted priors, PDTS offers a principled, efficient, and scalable alternative to boost both robustness and efficiency in learning under uncertainty. Whether you're training a robot, an AI assistant, or a simulation policy, PDTS makes your adaptation faster, robuster, and smarter.